前端开发 September 23，2018

HTML5 Canvas ：圆周运动进阶

回顾圆周运动

HTML5 Canvas：运动和轨迹中介绍了 圆周运动 的实现原理，回顾其计算方式为：

// (centerX, centerY) : 中心点坐标
// radius：旋转半径
// angle：旋转的角度

x =  centerX + Math.sin(angle) * radius
y =  centerY + Math.cos(angle) * radius

上面的公式表示：我们有已知的 中心点 坐标，已知的 旋转半径 和旋转后的控制点相对于 x 轴夹角，也就是 旋转角度 。然后，基于 旋转半径 和不断变化的 旋转角度 来计算出旋转后的控制点坐标。

但，有时候...

只知道中心点坐标和控制点坐标时

在以往的学习过程里，我们知道可以通过三角函数算出 两点间的距离 ，这就得出了我们需要的 旋转半径 ，于是迎刃而解：

var dx = point.x - center.x,
    dy = point.y - center.y,
    angle = Math.atan2(dy, dx),
    radius = Math.sqrt(dx * dx + dy * dy);

只知道控制点坐标和每一帧旋转的角度时

先给出控制点基于原点 (0, 0) 旋转的计算公式：

// rotation：角度增量，即在初始角度的基础上旋转的角度

x = x * Math.cos(rotation) - y * Math.sin(rotation);
y = y * Math.cos(rotation) + x * Math.sin(rotation);

之于为什么会推导出上面的公式？整个推导过程为：

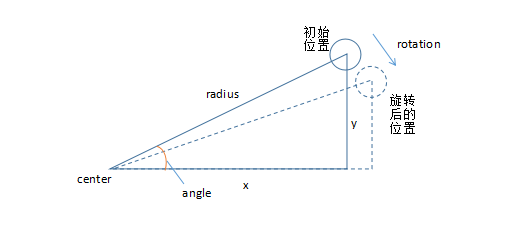
1.由上图可见，控制点的坐标可计算为：

x = radius * cos(angle);
y = radius * sin(angle);

2.旋转后，控制点的坐标可预测为：

// angle：初始角度，即处于初始位置的已知点与 x轴 的夹角角度
// rotation：角度增量，即在初始角度的基础上旋转的角度

x = radius * cos(angle + rotation);
y = raidus * sin(angle + rotation);

3.我们知道三角函数中包含一些常用的诱导公式，这里需要用到：

cos(a + b) = cos(a) * cos(b) - sin(a) * sin(b);
sin(a + b) = sin(a) * cos(b) + cos(a) * sin(b);

4.于是，将控制点的预测坐标公式展开：

x = radius * cos(angle) * cos(rotation) - raidus * sin(angle) * sin(rotation);
y = raidus * sin(angle) * cos(rotation) + raidus * cos(angle) * sin(rotation);

5.消除多余项，得出结论：

// 又因为 
// x = radius * cos(angle);  
// y = radius * sin(angle);  
// 将其代入，得出：

x = x * Math.cos(rotation) - y * Math.sin(rotation);
y = y * Math.cos(rotation) + x * Math.sin(rotation);

6.之前的推算可以看作是围绕原点 (0, 0) 旋转，所以，当我们可以将中心点置于坐标系中的任何一点，进而得出公式：

x = center.x + (x - center.x) * cos(rotation) - (y - center.y) * sin(rotation);
y = center.y + (y - center.y) * cos(rotation) + (x - center.x) * sin(rotation);

便于理解，我们可以想象为先将已知中心点坐标看作是原点，待控制点旋转后，再加上中心点距离真实原点的 x 轴、y 轴距离回归真实坐标系。

举个栗子：

<html>
<body>
    <canvas id="myCanvas" width="200" height="200" style="border: 1px solid">
        你的浏览器不支持canvas,请升级你的浏览器
    </canvas>
</body>
</html>
<script>
    (function () {
        // 准备画布
        var canvas = document.getElementById("myCanvas");
        var ctx = canvas.getContext("2d");

        // 规定已知的中心点和围绕中心点旋转的控制点
        var center = { x: 100, y: 100 };
        var point = { x: 50, y: 100 };

        // 规定没帧控制点在上一帧角度的基础上旋转 30 度
        var rotation = 30 * Math.PI / 180;

        setInterval(function () {
            ctx.clearRect(0, 0, 200, 200);

            // 计算圆周轨迹的每一个坐标
            var x = center.x + (point.x - center.x) * Math.cos(rotation) - (point.y - center.y) * Math.sin(rotation);
            var y = center.y + (point.y - center.y) * Math.cos(rotation) + (point.x - center.x) * Math.sin(rotation);

            point.x = x
            point.y = y

            // 画出小球
            ctx.beginPath();
            ctx.arc(point.x, point.y, 10, 0, 2 * Math.PI);
            ctx.fill();
            
            // 画中心
            ctx.beginPath();
            ctx.arc(center.x, center.y, 2, 0, 2 * Math.PI, true);
            ctx.fill();

        }, 100)
    })()
</script>